The Interest Rate, Present Value, and Future Value
During the Middle Ages in Europe, governments often banned lenders from charging interest on loans, partly because some people interpreted the Bible as prohibiting the practice and partly because most people believed that anyone with funds to spare should be willing to lend them to poorer friends and neighbors to purchase basic necessities without charging interest on the loan. In modern economies, households and firms usually borrow money to finance spending that has little to do with basic necessities. Perhaps as a result, charging interest on loans is no longer banned in most countries. Today, economists consider the interest rate to be the cost of credit
Why Do Lenders Charge Interest on Loans?
If apple growers charged a zero price for apples, very few apples would be supplied. Similarly, if lenders, who are suppliers of credit, didn’t charge interest on loans, there would be very little credit supplied. Recall from your introductory economics course the important idea of opportunity cost, which is the value of what you have to give up to engage in an activity. Just as the price of apples has to cover the opportunity cost of supplying apples, the interest rate has to cover the opportunity cost of supplying credit. Consider the following situation: You make a $1,000 loan to a friend who promises to pay back the money in one year. There are three key facts you need to take into account when deciding how much interest to charge him: (1) By the time your friend pays you back, prices are likely to have risen, so you will be able to buy fewer goods and services than you could have if you had spent the money rather than lending it; (2) your friend might not pay you back; in other words, he might default on the loan; and (3) during the period of the loan, your friend has use of your money, and you don’t. If he uses the money to buy a computer, he gets the use of the computer for a year, while you wait for him to pay you back. In other words, lending your money involves the opportunity cost of not being able to spend it on goods and services today. So, we can think of the interest you charge on the loan as being the result of
During the Middle Ages in Europe, governments often banned lenders from charging interest on loans, partly because some people interpreted the Bible as prohibiting the practice and partly because most people believed that anyone with funds to spare should be willing to lend them to poorer friends and neighbors to purchase basic necessities without charging interest on the loan. In modern economies, households and firms usually borrow money to finance spending that has little to do with basic necessities. Perhaps as a result, charging interest on loans is no longer banned in most countries. Today, economists consider the interest rate to be the cost of credit
Why Do Lenders Charge Interest on Loans?
If apple growers charged a zero price for apples, very few apples would be supplied. Similarly, if lenders, who are suppliers of credit, didn’t charge interest on loans, there would be very little credit supplied. Recall from your introductory economics course the important idea of opportunity cost, which is the value of what you have to give up to engage in an activity. Just as the price of apples has to cover the opportunity cost of supplying apples, the interest rate has to cover the opportunity cost of supplying credit. Consider the following situation: You make a $1,000 loan to a friend who promises to pay back the money in one year. There are three key facts you need to take into account when deciding how much interest to charge him: (1) By the time your friend pays you back, prices are likely to have risen, so you will be able to buy fewer goods and services than you could have if you had spent the money rather than lending it; (2) your friend might not pay you back; in other words, he might default on the loan; and (3) during the period of the loan, your friend has use of your money, and you don’t. If he uses the money to buy a computer, he gets the use of the computer for a year, while you wait for him to pay you back. In other words, lending your money involves the opportunity cost of not being able to spend it on goods and services today. So, we can think of the interest you charge on the loan as being the result of
- Compensation for inflation
- Compensation for default risk the chance that the borrower will not pay backthe loan
- Compensation for the opportunity cost of waiting to spend your money
Notice two things about this list. First, even if lenders are convinced that there will be no inflation during the period of the loan and even if they believe there is no chance the borrower will default, lenders will still charge interest to compensate them for waiting for their money to be paid back. Second, these three factors vary from person to person and from loan to loan. For instance, during periods when lenders believe that inflation will be high, they will charge more interest. Lenders will also charge more interest to borrowers who seem more likely to default. The reward lenders require for waiting to be repaid can also vary across time and across lenders.
Most Financial Transactions Involve Payments in the Future
We are all familiar with interest rates that are charged on car loans or school loans, and interest rates paid on assets such as certificates of deposit in banks. Actually, the interest rate is important to all aspects of the financial system because of the following key fact:Most financial transactions involve payments in the future.When you take out a car loan, you promise to make payments every month until the loan is paid off.When you buy a bond issued by General Electric, General Electric promises to pay you interest every year until the bond matures.We could go on to list many other similar financial transactions that also involve future payments. The fact that financial transactions involve payments in the future causes a problem: How is it possible to compare different transactions? For instance, suppose that you need to borrow $15,000 from your bank to buy a car. Consider two loans:
● Loan A, which requires you to pay $366.19 per month for 48 months
● Loan B, which requires you to pay $318.71 per month for 60 months
● Loan A, which requires you to pay $366.19 per month for 48 months
● Loan B, which requires you to pay $318.71 per month for 60 months
Which loan would you prefer? The interest rate provides a means of answering questions like this because it provides a link between the financial present and the financial future. In this case, even though Loan A has a higher monthly payment, it has a lower interest rate: The interest rate on Loan A is 8%, while the interest rate on Loan B is 10%.While the interest rate is not the only factor to consider when evaluating a loan, it is an important factor. To explore further how the interest rate provides a link between the financial present and the financial future and to understand how to calculate interest rates, like those on Loan A and Loan B, we need to consider two key ideas: compounding and discounting.
Compounding and Discounting
Consider an example of compounding. Suppose that you deposit $1,000 in a bank certificate of deposit (CD) that pays an interest rate of 5%.What will be the future value of this investment? Future value refers to the value at some future time of an investmentmade today. In one year, you will receive back your $1,000 principal which is the amount invested (or borrowed) and 5% interest on your $1,000, or:
Compounding and Discounting
Consider an example of compounding. Suppose that you deposit $1,000 in a bank certificate of deposit (CD) that pays an interest rate of 5%.What will be the future value of this investment? Future value refers to the value at some future time of an investmentmade today. In one year, you will receive back your $1,000 principal which is the amount invested (or borrowed) and 5% interest on your $1,000, or:
We can rewrite this compactly as:
If:
i = the interest rate
Principal = the amount of your investment (your original $1,000) FV = the future value (what your $1,000 will have grown to in one year) then we can rewrite the expression as
i = the interest rate
Principal = the amount of your investment (your original $1,000) FV = the future value (what your $1,000 will have grown to in one year) then we can rewrite the expression as
(Note that we add the subscript 1 to FV1 to indicate that we are looking at the future value after one year.) This is an important relationship: It states that we can calculate a future value in one year by multiplying the principal invested by 1 plus the interest rate. Compounding for More Than One Period Suppose that at the end of one year, you decide to reinvest in—or roll over—your CD for another year. If you reinvest your $1,050 for a second year, you will not only receive interest on your original investment of $1,000, you will also receive interest on the $50 in interest you earned the first year. Economists refer to the process of earning interest on interest as savings accumulate over time as compounding. Compound interest is an important component of the total amount you earn on any investment. We can calculate the future value after two years of your initial investment
[Amount You Earned After One Year] * (Compounding During the Second Year) = Future Value after Two Years We can write this expression more compactly as:
We could continue to compound your initial $1,000 investment for as many years as you choose to roll over your CD. For instance, if you rolled it over for a third year at the same interest rate, at the end of the third year, you would have:
Note that the exponent on the compounding factor (1 + 0.05) equals the number of years over which the compounding takes place. It’s useful to generalize our result: If you invest $1,000 for n years, where n can be any number of years, at an interest rate of 5%, then at the end of n years, you will have

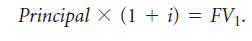


No comments:
Post a Comment